matlbpotlib trick
1. Figure
1.1. 分辨率
默认情况下,matplotlib将。默认情况下,matplotlib将提供640 x 480像素的图片文件,即4:3的横纵比。下面是改变了dpi和尺寸后具体的像素大小变化:
plt.figure(1)
# <Figure size 640x480 with 0 Axes>
plt.figure(1, dpi=300)
# <Figure size 1920x1440 with 0 Axes>
plt.figure(3, dpi=300, figsize=(3,4))
# <Figure size 900x1200 with 0 Axes>
2. color
2.1. colormap 色表
最全的色表:Colormap reference
对于具有正负值,特别是需要归零的图表,最好的选择就是发散色表,其中比较特别的是coolwarm的零值是灰色,非常好用。
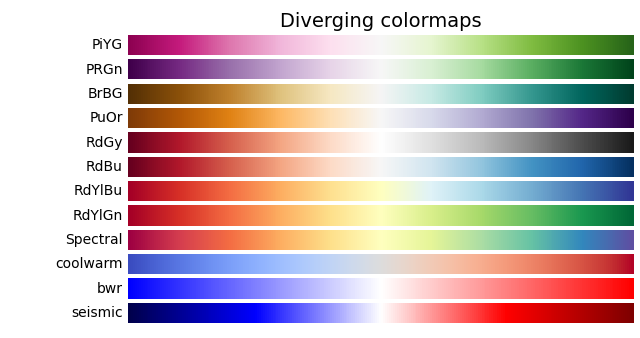
另外,在颜色图的名称后加_r可以获得反转版本。
2.2. colorbar 色条
fig.colorbar(mappable, ax=ax, location='right', anchor=(0, 0.3), shrink=0.7)
常用的大概就是这些,location很好理解,shrink就是缩放的量,剩下比较抽象的是anchor:
anchor(float, float), optional The anchor point of the colorbar axes. Defaults to (0.0, 0.5) if vertical; (0.5, 1.0) if horizontal.
看了还是看不懂,不过实际体验是,当colorbar在右边的时候,x越大越靠右,y越大越靠上,主要还是试一试吧。
- 芝士Colorbar的例子:Colorbar - matplotlib Examples
- 芝士Colorbar的api:matplotlib.figure
2.3. Colormap Normalization 色表映射正规化
matplotlib真是太神奇辣!这是我觉得最好用的功能,没有之一(想到我之前还手动写 norm = plt.Normalize(norm_lim, -norm_lim) 这种代码就流泪)。
按照我的理解,凡是可以放
cmap参数的地方,都可以放上一个norm
2.3.1. Centered 居中
最常用的应该是这个,特别是在正负值都有,而零值需要居中的情况下
pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
2.3.2. Symmetric logarithmic 居中的对数
这个简直是神中神!它既居中,又可以对数,最关键的是,由于0对数密度无穷大,这个正规化提供了零值附近的线性部分(Since the logarithm of values close to zero tends toward infinity, a small range around zero needs to be mapped linearly)。搞了很久终于弄懂了,现在进行一个记录
pcm = ax[0].pcolormesh(X, Y, Z,
norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
vmin=-1.0, vmax=1.0, base=10),
cmap='RdBu_r', shading='auto')
比较好理解的几个参数有:base是对数底数;vmin/vmax是轴的上下限;linthresh是线性映射的范围,绝对值超过linthresh的部分是对数映射的。
linscale这个东西就比较神秘:
The size of this range in the colormap is set by linscale. When linscale == 1.0 (the default), the space used for the positive and negative halves of the linear range will be equal to one decade in the logarithmic range.
one decade这个东西就很神秘对吧,导致这段话完全看不懂,但实际上指的是刻度的间距:
# 从左到右对应下面的三个正规化bar
norm1 = colors.SymLogNorm(
linthresh=10**10, base=10, vmin=-10**12, vmax=10**12, linscale=1
)
norm2 = colors.SymLogNorm(
linthresh=10**11, base=10, vmin=-10**12, vmax=10**12, linscale=1
)
norm3 = colors.SymLogNorm(
linthresh=10**11, base=10, vmin=-10**12, vmax=10**12, linscale=2
)
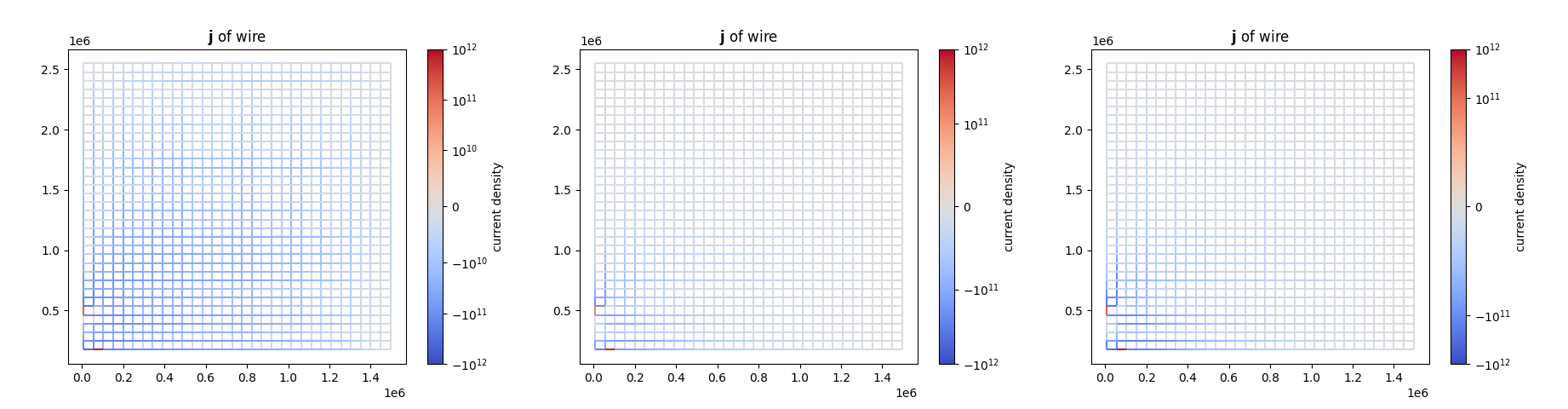
norm1和norm2有参数linscale=1,可以看到刻度都是均匀的;而norm3有参数linscale=2,0到$\plusmn 10^{11}$的间距就是对数轴那边的两倍。
那明白了这些之后,就可以通过调节linthresh和linscale对可视化的焦点进行调整:linthresh越大,越多的数据落在线性区,进而使零值附近的值变得“模糊”;linscale越大,留给对数区的范围越小,使得极值附近的值变得更加“鲜艳”。这样就可以调节图的焦点了。
3. 2D
3.1. 如何在 matplotlib 中绘制二维结构化网格
How to plot a 2d structured mesh in matplotlib
不仅仅是mesh,多段复杂连线都可以使用lineCollection完成,lineCollection使用的数组形式为(线,点,坐标),其中同一线下的点按顺序连接,不同线下的点不互联,因为坐标是二维的,数组尺寸必然为(l,n,2)。
下面的代码并非OOC代码,实际上Axes对象下也有add_collection方法,方法会返回一个对象,对该对象调用remove可以将其从图上移除。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
x, y = np.meshgrid(np.linspace(0,1, 11), np.linspace(0, 0.6, 7))
segs1 = np.stack((x[:,[0,-1]],y[:,[0,-1]]), axis=2)
segs2 = np.stack((x[[0,-1],:].T,y[[0,-1],:].T), axis=2)
plt.gca().add_collection(LineCollection(np.concatenate((segs1, segs2))))
plt.autoscale()
plt.show()
3.2. 给网格(线段)按值上色
使用set_array方法:
lc = LineCollection(segments, cmap='viridis', norm=norm)
lc.set_array(dydx)
3.3. 给网格(线段)上渐变色
对不起,做不到。
如果使用lineCollection就不可避免地是每根线一个颜色,这没有什么办法,只能通过细分线进行假渐变。要么就是散点移动产生渐变,还有一个用pcolormesh的奇技淫巧,剩下的没有仔细看,目前没有找到好的解决方案。
3.4. 画圆
参考plot a circle with pyplot - stackoverflow可以得到基本的画圆的方法如下:
circle = plt.Circle((1, 1), 0.2, color='g', clip_on=False)
ax.add_patch(circle1)
参考Why is matplotlib plotting my circles as ovals - stackoverflow可以用一些方法去解决画圆变形的困难,例如ax.axis("equal")
3.5. 确定图层
在多种元素绘图的时候经常出现图层重叠的情况,这个时候需要使用到的关键字参数是zorder
参考Zorder specification in matplotlib patch collections - stackoverflow
例如对于Circle类:
circle = Circle(
(info["xpos"], info["ypos"]),
radius=radius,
color=color,
fill=False,
zorder=10000,
)
同样对于Circle的集合CirclePatch也有(此时Circle本身的zorder会被覆盖):
circ.append(Circle ((1,1), 0.2))
coll=PatchCollection(circ, zorder=10)
4. 3D
4.1. 使用XYZ一维数组/散点绘制三维平面
首先说明为什么 fig.subplots(subplot_kw=dict(projection="3d")) 不能使用:一般的3d plot实际上是四边形绘图,不是网格化的X、Y不保证能进行四边形渲染。因此,解决方案是进行三角形渲染,即使用plot_trisurf